Queridos lectores,
 El ingeniero Samuel Laboy Alvarado nació en Lajas, un pequeño pueblo en la Isla de Puerto Rico. Realizó sus estudios universitarios en el Colegio de Agricultura y Artes Mecánicas en Mayagüez, en donde obtuvo en 1958, el Bachillerato en Ingeniería Civil. En 1970, recibió su grado de Maestría en Ingeniería Civil en la Universidad del Estado de Oklahoma, en Stillwater. Laboy trabajó por 32 años en el Gobierno de Puerto Rico. Durante su trayectoria de empleado gubernamental, recibió cuatro nominaciones para recibir el Premio Manuel A. Pérez, considerado el máximo premio de reconocimiento por trabajos extraordinarios que ofrece el Gobierno de Puerto Rico a sus empleados. Laboy recibió el codiciado premio en tres de las cuatro nominaciones. Sirvió como oficial militar en las Fuerzas Armadas de Estados Unidos. Como inventor, ha recibido tres patentes de la oficina de Patentes de Estados Unidos. Como autor, tiene publicados cinco libros sobre las pirámides de Egipto, y es considerado como un estudioso e investigador incansable.
El ingeniero Samuel Laboy Alvarado nació en Lajas, un pequeño pueblo en la Isla de Puerto Rico. Realizó sus estudios universitarios en el Colegio de Agricultura y Artes Mecánicas en Mayagüez, en donde obtuvo en 1958, el Bachillerato en Ingeniería Civil. En 1970, recibió su grado de Maestría en Ingeniería Civil en la Universidad del Estado de Oklahoma, en Stillwater. Laboy trabajó por 32 años en el Gobierno de Puerto Rico. Durante su trayectoria de empleado gubernamental, recibió cuatro nominaciones para recibir el Premio Manuel A. Pérez, considerado el máximo premio de reconocimiento por trabajos extraordinarios que ofrece el Gobierno de Puerto Rico a sus empleados. Laboy recibió el codiciado premio en tres de las cuatro nominaciones. Sirvió como oficial militar en las Fuerzas Armadas de Estados Unidos. Como inventor, ha recibido tres patentes de la oficina de Patentes de Estados Unidos. Como autor, tiene publicados cinco libros sobre las pirámides de Egipto, y es considerado como un estudioso e investigador incansable.
Su mayor logro como profesional ha sido el descubrimiento del origen y diseño geométrico utilizado por los egipcios para realizar el diseño de sus pirámides, en especial, el de la Gran Pirámide. Cuando Laboy terminó sus estudios de maestría en la Universidad, se comprometió con él mismo de usar el tópico la “Solución de la Geometría de la Gran Pirámide de Egipto” en su tesis para sus estudios. A pesar de no poder proseguir sus estudios doctorales, comenzó, y continuó usando los requisitos aplicables a las tesis universitarias, hasta terminar en el 2008. Sus estudios fueron basados con base a requisitos y principios científicos, y técnicos, que le proveen la debida credibilidad y exactitud.
Laboy reside en la actualidad en Guaynabo, donde continúa trabajando en sus investigaciones sobre las pirámides.
Son numerosos los libros y documentales presentados a través de los tiempos, sobre la Gran Pirámide de Egipto. Muchos de ellos tienen su base en seres extraterrestres, otros en conceptos del espacio y las estrellas, algunos en conceptos religiosos, pero todos basados en teorías. A muchos les falta información valida, otros contienen algunos errores en conceptos matemáticos y geométricos.
La información existente sobre la historia y construcción de la Gran Pirámide, nos llega de Heródoto, un historiador griego que visitó el país de Egipto cerca de 680 años antes del nacimiento de Cristo. La información que Heródoto ofrece es muy interesante. Por ejemplo, Heródoto narra en sus escritos, lo que le contaron en su época, sobre la construcción de las pirámides. Relata que la Gran Pirámide fue construida durante el reinado del faraón Cheops, e indica que Cheops fue un faraón muy cruel con su gente. Les cerró los templos que utilizaban para sus servicios religiosos, prohibió la celebración de sus acostumbrados ritos y sacrificios y los puso a trabajar en la construcción de la Pirámide. La comunidad egipcia de ese tiempo fue organizada en diferentes grupos. Unos cortaban las piedras en las canteras, otros las transportaban y finalmente, los que las colocaban en la pirámide.
Según el historiador, siempre había 100,000 obreros trabajando en las diferentes fases de la construcción, los cuales eran relevados cada tres meses. Aprendió de sus antiguos maestros, que la construcción del camino para transportar los bloques de piedra y la construcción de la Cámara Subterránea, les tomó 10 años. Por otro lado, la construcción de la estructura de la pirámide tomó veinte años adicionales, es decir, 30 años en total.
EL dato de que las excavaciones subterráneas tomaron 10 años, aparenta ser muy exagerado y poco creíble sobre el tiempo utilizado para realizar las excavaciones subterráneas que él señala. El trabajo consistió en la construcción de una sección del pasadizo de descenso, de la construcción de su componente horizontal y la cámara subterránea. La cámara subterránea fue construida rústicamente, es decir, se hizo sin terminaciones de construcción y hasta tiene la apariencia de haber sido dejada a medio construir. El indicar que tomó 10 años en realizar esa limitada construcción resulta muy raro. Tal vez es una indicación de que el diseño también incluía la construcción secreta de una gran cámara la cual no se menciona en ese evento. Me refiero a algo como la real construcción de la verdadera Cámara Mortuoria para el Faraón Cheops y sus tesoros. Debemos recordar que Heródoto también señala que la Cámara Mortuoria del Faraón era una subterránea y que su momia descansaba sobre una isleta central, rodeada de agua, proveniente del Río Nilo.
Por otro lado, la altura calculada para la Gran Pirámide, cuando finalizada, desde su base al proyectado ápice, es de un poco más de 480 pies. A base de 10 pies por piso, podríamos compararla con un edificio de 50 pisos cuando fue terminada. La pirámide es truncada, o sea, le falta parte de su cúspide. Se desconoce si esa parte fue construida, o destruida de alguna forma posteriormente. Actualmente le faltan aproximadamente 30 pies para llegar a su ápice o punta. De igual forma, podríamos mencionar que el trabajo de excavación bajo la base de la pirámide, hasta donde se conoce, se hizo hasta una profundidad de aproximadamente 100 pies, lo cual equivalente a la altura de un edificio de 10 pisos. Como ya indicado, se construyeron pasadizos, la Cámara Subterránea y con una gran probabilidad, la verdadera Cámara Mortuoria del Faraón Cheops. En general, la ciencia de la Egiptología tiene muy pocos registros reales sobre los tiempos de la Cultura Egipcia con anterioridad a los 680 años A. C., o sea, existen pocos datos y además, poco confiables sobre la época de la construcción de las pirámides.
Unidades de medidas usadas por los egipcios
Las medidas de la base de la pirámide están definidas como 755.7488 pies en el sistema inglés, pero también han sido medidas, o estimadas como 440 codos en el sistema de medidas egipcio. Si se establece la proporción de 755.7488 pies / 440 codos, tendríamos 1.717610909 pies por cada codo, que al multiplicarse por 12 pulgadas el número de conversión sería de 20.61133091 pulgadas por codo.
En los primeros estudios geométricos de la Gran Pirámide por John Taylor (en 1851) y otros, se introduce el concepto de Pi (π) = 3.14159…, en las fórmulas de las pirámides. De ahí se dedujo, erróneamente, que el perímetro de la base P = 4 (b), era igual a la circunferencia del círculo C = π (D), o sea, que C = P. Este concepto pone el valor del Perímetro de la base igual a (4 b) = (π D), o sea, el valor de π resulta = (4) (b) / D = 3.144605418, lo cual sabemos que no es el correcto.
Sabemos que el perímetro de la Gran Pirámide de acuerdo a Sir W. Petrie, famoso egiptólogo, y que realizó un estudio e informe sobre la geometría de la Gran Pirámide en 1881, es igual a 755.7488 (4) = 3,022.9952 pies. Por tanto, usando el círculo, el diámetro tendría que ser igual a (3,022.9952 / π) = 962.249258, y la altura de la pirámide resultaría ser igual a 481.1246 pies. Pero sabemos que la altura es 480.6637 pies, la diferencia es de apenas 0.460953 pies, es decir, 5.53 pulgadas. Por otro lado, la tangente inversa de la proporción (D / b) corresponde al ángulo de las caras de la pendiente de la pirámide, en este caso sería igual 481.1246 (2) / 755.7488 = 1.2732396, cuya tangente inversa es 51° 51’ 14.3” que es el ángulo que mucha gente, y por mucho tiempo, asumió que corresponde a la Gran Pirámide y la gente pensó que el diseño cuadraba la longitud del círculo con la circunferencia de su base. No obstante, ese concepto ha sido ya desestimado.
EL SIMBOLO PERFECTO
En mi caso, al examinar el “Símbolo Perfecto” y comparar sus propiedades con las de la Gran Pirámide, noté que el símbolo me daba el ángulo de las caras ya definido, no tenía que calcularlo o estimarlo. En el diseño del símbolo, la pendiente del ángulo representa resulta ser igual a la raíz cuadrada de f, es decir, Öf = 1.27201965. Por tanto, el ángulo de las caras es igual a 51° 49’ 38.25”. Por consiguientes, utilizando la medida más segura de las mensuras de Petrie, la de los lados de la base de la pirámide con 755.75 pies, calculé el valor de la altura, la cual resulta ser igual a 480.6637 pies.Esta altura no es la actual de la pirámide, pues es truncada. Le falta parte del ápice, el cual se desconoce si fue que no se construyó o que fue destruido de alguna forma desconocida.
La circunferencia (C) del círculo esπ (D) = 3,020.0989 pies, y el perímetro de la base P = 4 b = 3,022.9952. La diferencia entre la circunferencia (C) y el perímetro (P) es 2.8963 pies, digamos, cerca de 35 pulgadas.
Como algo predestinado, y que deseo aprovechar para dar testimonio de ello, ya sabía del número 480.6637 pies, pues desde antes de empezar mis estudios piramidales, algo extraño me había señalado que la altura de la Gran Pirámide era definida por el producto del número 153 pies y el valor de Pi =π = 3.1415926. En otras palabras, la altura de la Gran Pirámide la podríamos definir también como igual a 153 π = 480.6637 pies. Curiosamente, y a modo de información, la altura de la Pirámide de Chephren, la segunda en tamaño en Giza, está definida por el producto de 150 pies y π = 471.24 pies.
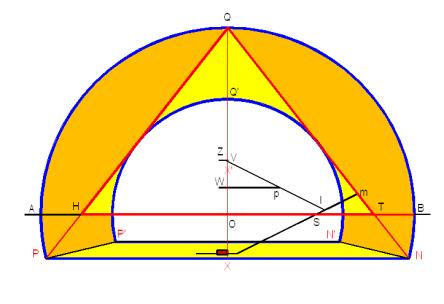
Un dato muy importante sobre la Gran Pirámide mencionado por Heródoto en sus escritos es que indica que los antiguos historiadores sobre las pirámides le indicaron que la estructura de la Gran Pirámide se construyó de tal forma, que el cuadrado de su altura es exactamente igual al área de la superficie triangular de sus caras.
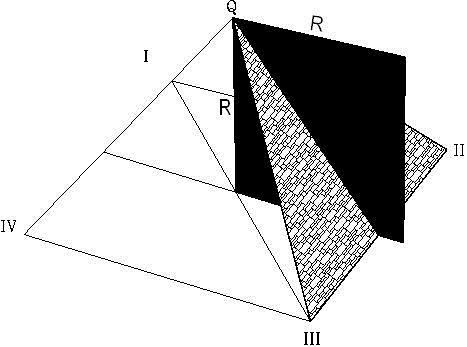
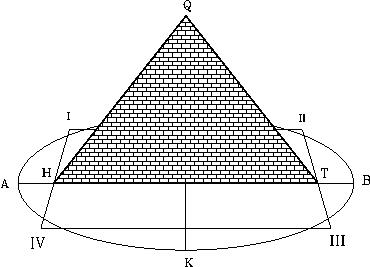
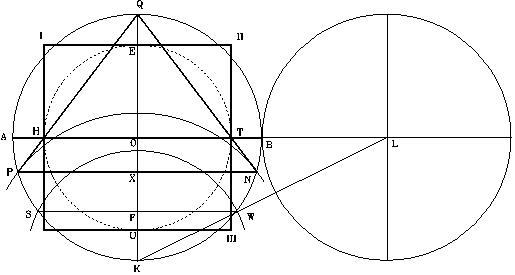
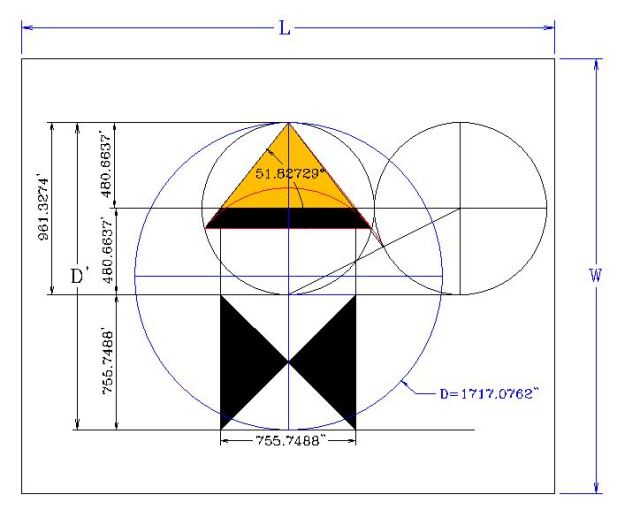
Este dato es muy interesante. La figura A, muestra el cuadrado de la altura pintado en negro, mientras la figura B, muestra ensombrecida el área superficial de una de sus caras. Según las especificaciones geométricas del diseño de la pirámide, las únicas especificaciones heredadas de la antigüedad para reconocer la estructura geométrica de la Gran Pirámide, las podemos comprobar fácilmente en mi diseño de la pirámide la cual cumple con estos requisitos.
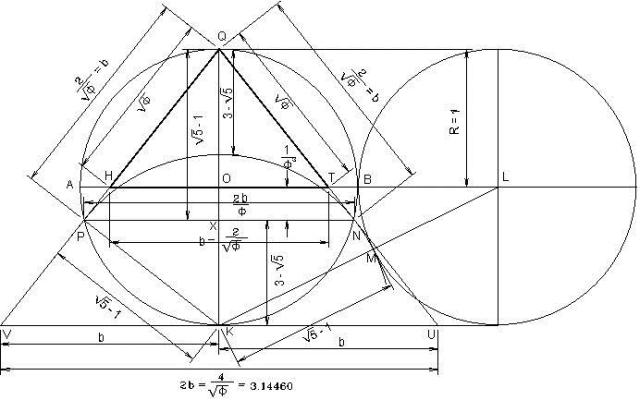
En la figura A, se muestra el área inclinada entre los puntos Q, II y III y en la figura B, se muestra el cuadrado creado con la altura de la pirámide. Según Heródoto, le informaron que estas dos áreas son exactamente iguales. El área de la superficie de la cara puede ser calculada como la mitad del largo de la base multiplicado por la distancia inclinada desde el centro de la base al tope de la pirámide. El largo (b) de la base es equivalente a (D / Öf), y la distancia inclinada de la base al tope (h’) = R Öf. Por lo tanto el área de su superficie es (1 / 2) (D / Öf) (R Öf), esto es, (D) (R) / 2 = (R) (R) = R². Por otro lado, el cuadrado de la altura es igual a R². Esto confirma que lo que le dijeron a Heródoto era correcto, las áreas son iguales: R² = R².
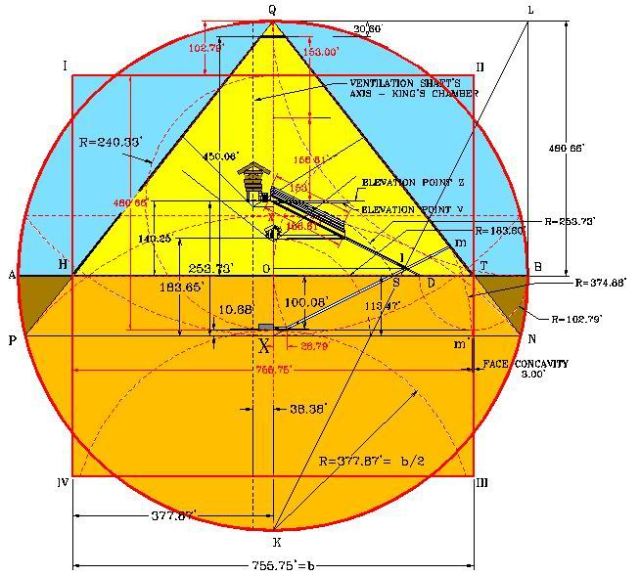
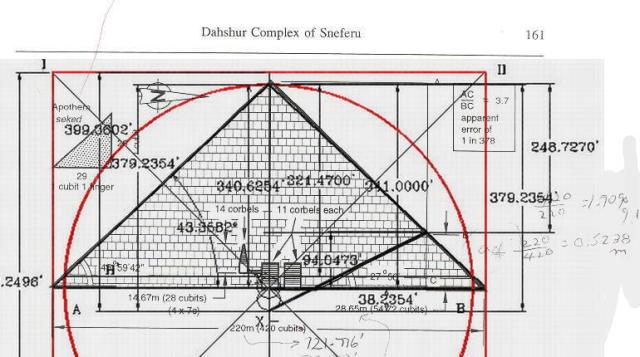
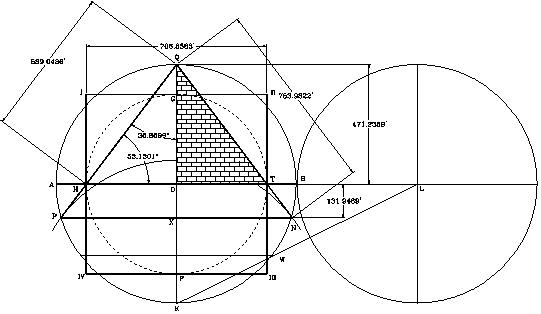
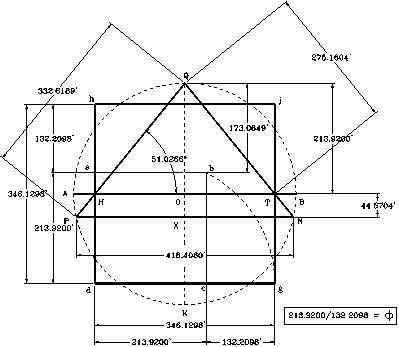
La figura ilustrada muestra un esquema de la composición geométrica de la Gran Pirámide. Luego de transcurridos cerca de 4,700 años, solo se ha determinado que la pirámide tiene una altura de aproximadamente 480 pies y mide cerca de 756 pies en cada lado, de su base cuadrada. Sus lados inclinados, desde su tope hasta el centro de la base en el pavimento (apotema), miden 611.41 pies en cada lado.
Este es el panorama que se nos presenta en la actualidad en relación al plano de construcción de la Gran Pirámide. El plano original nunca ha sido encontrado, ni nadie ha podido diseñarlo. Hace más de 40 años me di a la tarea de estudiar su estructura y dedicar gran parte de mi tiempo a descubrir la geometría envuelta en su diseño. A mi entender, como ingeniero civil, los trazos de las líneas exteriores de la estructura, y los interiores que establecen los pasadizos, cámaras, y corredores, me indicaban que su estructura tenía que seguir algún patrón arquitectónico geométrico de diseño, el cual le serviría de marco al diseñador para el desarrollo del plano de su obra, y que por ende, enmarcaría toda la estructura del monumento, incluyendo sus diseños subterráneos.
Mucha gente ha sugerido las figuras del círculo, el triángulo y el cuadrado como partes de su diseño. No obstante, se desconoce cómo crearlos y utilizarlos en los diseños. Cada figura geométrica varía en tamaño y se requerirían formulas diferentes. También habría que definir sus fórmulas matemáticas, características y propiedades de enlaces. Mi idea era mucho más profunda. Me tomó varios años en investigar crear, inventar, o tal vez reinventar, el patrón arquitectónico de diseño que yo tenía en mente habían utilizado los egipcios para su diseño.
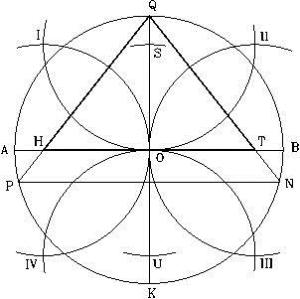
Luego de varios años de estudios, y búsqueda del mencionado patrón geométrico sin éxito, desarrollé el patrón arquitectónico geométrico deseado, el cual consistía de la combinación de las 3 figuras geométricas mencionadas, el círculo, el triángulo y el cuadrado pero utilizando únicamente como instrumentos de diseño, un compás para trazar las líneas curvas y una regla lineal para trazar las líneas rectas. Por consiguiente, no utilicé números, cálculos matemáticos, o fórmulas en su creación. Por tanto, el patrón arquitectónico diseñado no tenía unidades de medida. Comprobé que reunía mis especificaciones y servía para mis propósitos de diseño. Al examinar sus características y propiedades, me resultó perfecto para diseñar pirámides y otras otros tipos de diseños, como de pinturas, estatuas, joyería, edificios, salones, etc. Era tan perfecto en sus propiedades que lo llamé el “Símbolo Perfecto”. Era un patrón arquitectónico perfecto para que los ingenieros egipcios pudieran diseñar sus pirámides y muchas de sus múltiples obras de arte y de construcción.
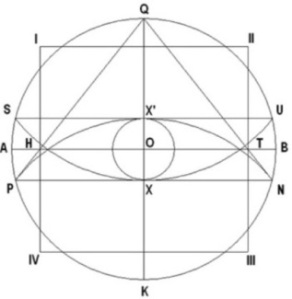
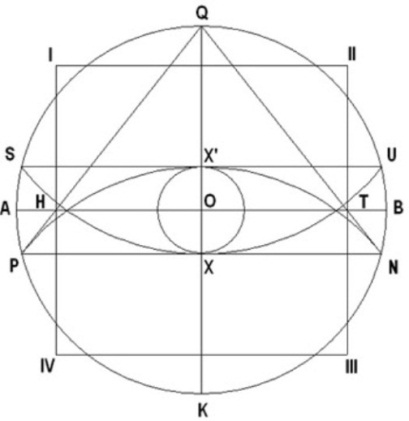
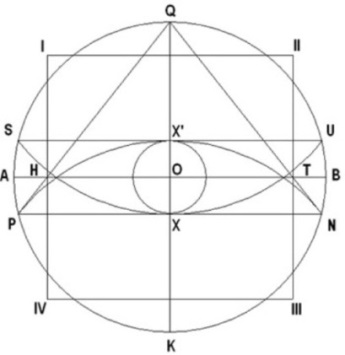
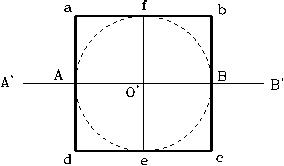
Puedo señalar que el arreglo geométrico que exhibe el “Símbolo Perfecto” y que consiste de un círculo, un triángulo y un cuadrado, entrelazados de forma especial, no tiene relación alguna con el diseño geométrico de las pirámides, ya que puede ser trazado en cualquier parte del mundo sin hacer referencia a las pirámides. Esto indica que su diseño es generado por el Creador y Gran Matemático del Cosmos, en su departamento de Geometría. Resulta que mediante ese símbolo tan sencillo, se han podido diseñar y edificar las pirámides Egipcias. Pero que también las de otras culturas ancestrales de nuestro globo terráqueo. En mis libros presento evidencia que tanto las pirámides egipcias y otras antiguas construcciones mundiales tienen su origen en la configuración geométrica que nos ofrece el Símbolo Perfecto. He aquí, la figura a la que me refiero, y la forma de construirlo.
PATRON GEOMETRICO ARQUITECTONICO
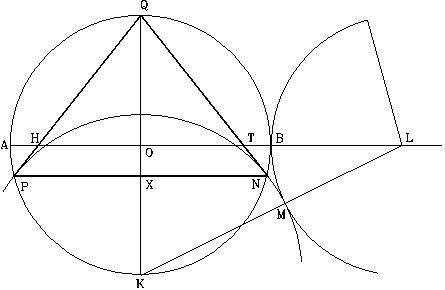
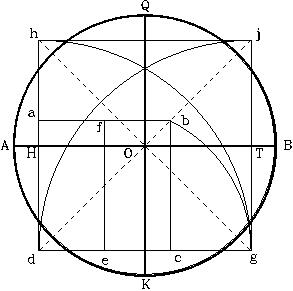
CONSTRUCCION GEOMETRICA DEL SIMBOLO PERFECTO Y QUE REPRESENTAN LOS TRABAJOS EN AGRIMENSURA NECESARIOS PARA CONSTRUIR LA GRAN PIRAMIDE
El proceso para diseñar el Símbolo Perfecto es igual al utilizado sobre el terreno, para definir los trabajos de agrimensura para la construcción de la Gran Pirámide
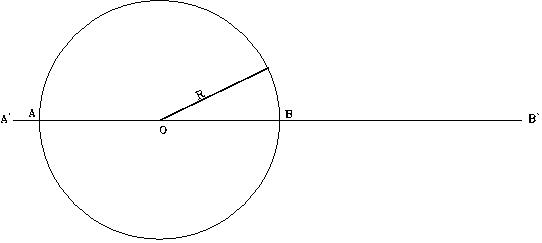
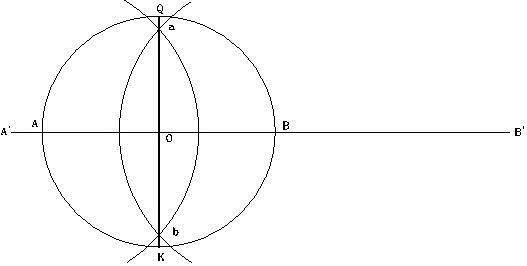
En cualquier punto de la línea, trazar un círculo de cualquier radio, el radio representa la altura de la pirámide.
Es importante hacer notar que el tamano de los lados del cuadrado y sus esquinas lo establece el mismo procedimiento del diseño. El tamaño del cuadrado aumenta, o disminuye, al cambiarse el radio del circulo.
El Símbolo Perfecto puede ser trazado utilizando la figura de cualquier círculo, no importa su tamaño. Es creado sin la necesidad de números, o cálculos matemáticos, Se crea mediante un proceso geométrico. Sus dimensiones son proporcionales al radio del círculo. Quiere decir se puede aumentar, o disminuir su tamaño, variando únicamente el valor que se le atribuya al radio del círculo. Otra virtud que tiene es que se puede utilizar cualquier unidad de medida para el radio del círculo, sea en codos egipcios, metros, pies, pulgadas centímetros, o cualquiera otra unidad de medida que se interese. Los resultados de sus dimensiones serán expresados en la misma unidad de medida utilizada para el radio. Es importante hacer notar que solamente se necesita el número y unidad de medida del radio del círculo, para definir las dimensiones de todo el diseño que se haya creado. Pongamos a prueba su utilidad.
UN DISENO MODELO DE LA GRAN PIRAMIDE
Mediante el siguiente ejercicio me propongo probar que esta figura geométrica, es el origen de la Gran Pirámide de Egipto y que su diseño enmarca el diseño y la construcción de esa Pirámide.
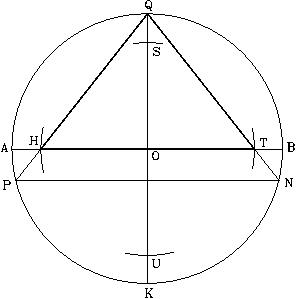
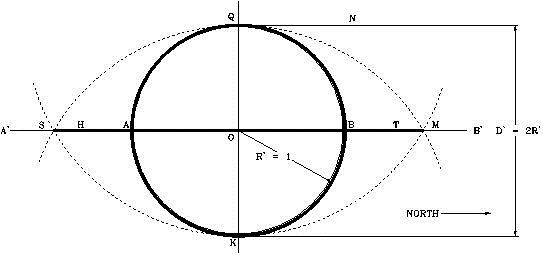
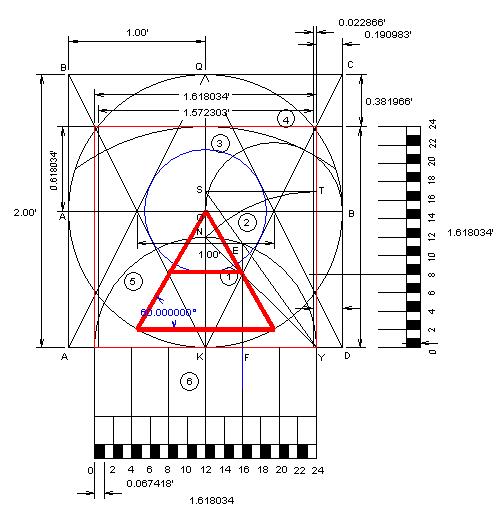
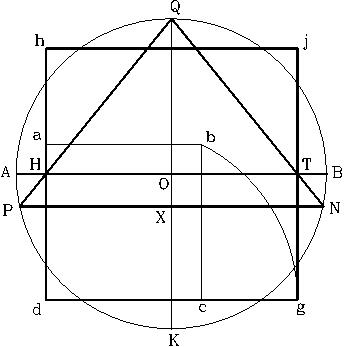
Al observar el símbolo, este nos sugiere mediante el triángulo, lo que parece ser la configuración de una pirámide, y que podemos designar como “pirámide modelo”. Para definir y relacionar este modelo con la Gran Pirámide, podemos establecer las siguientes especificaciones geométricas:
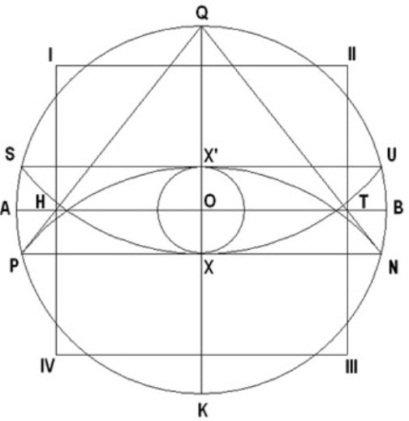
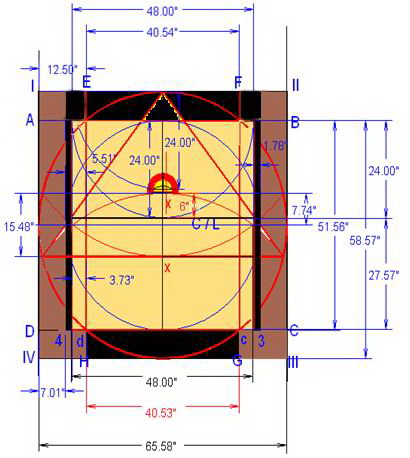
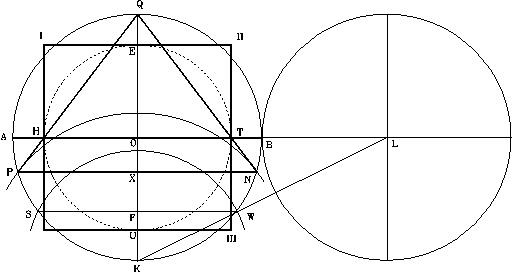
Según dicho, las dimensiones del símbolo son proporcionales al tamaño del radio (QO) del círculo, y que también corresponde a la altura de la pirámide, designada como modelo. El diámetro horizontal (AB) del círculo, corresponde al nivel del terreno sobre el cual se construirá la pirámide, el diámetro vertical (QK) corresponde al eje vertical de la pirámide, y el triángulo (QHT) corresponde a la sección vertical de la pirámide, vista a través de su eje central (QK). El área entre los puntos (P, H, T, y N) representa el área del terreno debajo de la pirámide, donde se diseñarán y construirán las cámaras y pasadizos subterráneos de la “pirámide modelo”. Esta área no es observable ni está identificada en ninguno de los diagramas que se han realizado de la Gran Pirámide. No obstante, el símbolo nos la presenta como el área designada para enmarcar los trabajos subterráneos.
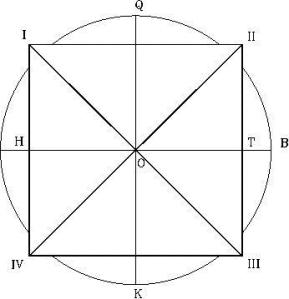
Nótese que existen dos puntos identificados en el símbolo como X y X’, los cuales tienen una función muy especial e importante, como se mostrará más adelante. El cuadrado entre los puntos (I, II, III, y IV) corresponde a una representación vertical de la base de la pirámide.
Con estos simples datos, podemos diseñar el plano de la “pirámide modelo” ilustrada en el Símbolo Perfecto y se demostrará que es el origen y que representa el diseño geométrico que tiene la Gran Pirámide.
Veremos cómo, la figura del símbolo nos provee la información correcta y necesaria para calcular las dimensiones “del modelo de pirámide correspondiente a la Gran Pirámide. El único valor que se introducirá en este ejercicio será el que se asumirá para el radio del círculo para calcular todo el diseño creado, exterior e interior de la pirámide. ¿Increíble, no?
Si cambiamos el valor del radio, aunque sea por varias pulgadas, todas las dimensiones cambiarán y se estará representando otra pirámide, que aunque será proporcionar a la Gran Pirámide, tendrá dimensiones diferentes. Solo existe una medida de altura (o del radio) que satisface el número necesario para generar todas las dimensiones correctas para la Gran Pirámide. Esta es igual al producto de 153 pies y el valor de la función de π, o sea, 480.6637 pies. Esta es la única unidad de medida para el radio, que satisface el generar todas las dimensiones de la Gran Pirámide. Esta puede ser convertida a otras unidades equivalentes de medidas, y los resultados serán correctos, basados en esas nuevas unidades de medida. Podemos mencionar entre ellas: codos egipcios como se usaban en Egipto, metros, pies, pulgadas, o cualquiera otra unidad de medida que se desee usar para el radio. En cada caso, los resultados a obtenerse estarán expresados en la misma unidad de medida utilizada para el radio del círculo y los diseños a crearse serán iguales en todos los casos, pero con diferentes unidades de medida.
En nuestro ejemplo, como las medidas inglesas con unidades de pies y decimales son las más conocidas y que además, que muchas personas no conocen o están relacionadas con las unidades de codos egipcios, usaremos las unidades inglesas de pies y pulgadas. Muchas personas creen que la pirámide tiene que ser diseñada usando codos egipcios, pues eran las unidades de medida que ellos usaron. Pero recuerden, en una estructura ya construida sus dimensiones están fijas, no son variables. No importa las unidades de medida que se usen para medirlas la estructura no cambiará, sólo sus unidades de medida.
En este interesante caso, tenemos que determinar entre millones de números y sus unidades de medidas que existen, cuál de ellas satisface el valor para el radio del circulo que genere las dimensiones correctas para la Gran Pirámide. Para hacer más interesante y curioso nuestro ejemplo, tomaremos el valor del radio del círculo, igual al producto de dos números; el enigmático número 153 y el de la función de Pi (π = 3.154159…). El producto de estos dos números, 153 () es igual a 480.6637 expresado en pies. El por qué utilizar el producto del número 153 y el de la función de Pi, será explicado adelante. Para evitar la presentación de muchos cálculos matemáticos en este documento, se presentarán únicamente sus resultados, los cuales han sido ya verificados en muchas ocasiones, incluyendo análisis con computadoras.
Existen diferentes medidas publicadas para la altura de la Gran Pirámide, que dependen de quien las calculó y entre qué puntos. Como es conocido, la pirámide carece de su ápice para poder obtenerse su altura vertical real. El tope de la pirámide nunca fue construido, o de alguna manera fue destruido, faltan cerca de 30 pies para llegar al tope.
Para probar definitivamente que la altura usada para mi plano de la pirámide modelo es la correcta, podemos compararla con la calculada por Sir W. M. Flinders Petrie, arqueólogo británico muy respetado en su profesión, que realizó un estudio bien detallado de toda su estructura piramidal. Petrie calculó la altura en 5,776 pulgadas, más o menos 7 pulgadas. O sea, entre 5,769 y 5,783 pulgadas. Es decir que su altura podría estar entre 480.75 y 481.916 pies. Sin embargo, el asumió un ángulo de 51° 52’, más o menos 2’, correspondiente a las caras.
Pero hay otro dato muy importante, Petrie indica que la medida más precisa que pudo obtener en su estudio fue la de los lados de la pirámide, que fue igual a 9,068.8 ±.5 pulgadas (esto es, la medida sería correcta entre 755.70 pies a 755.77 pies). Como el resultado de la altura para el modelo que diseñé es igual a 755.7488 pies, que representa el promedio de las medidas de Petrie, podemos decir que mi medida de los lados corresponde exactamente a la tomada físicamente por Petrie en la estructura.
Por otro lado, si Petrie hubiese calculado el ángulo de la pirámide con sus propios resultados, hubiese podido informar un resultado más exacto. Por ejemplo: Si la fórmula del ángulo es igual (D / b), tenemos 480.75 (2) / 755.75 = 1.272246113. La tangente inversa correspondiente a esta proporción es igual a 51.83224799° = 51° 49’ 56”, ángulo que es mucho más acertado que el que informó de 51° 52’.
El ángulo de las caras de la pirámide = 51.82729319° = 51° 49’ 38.25”. De esta forma, se comprueba que la estructura exterior de la Gran Pirámide corresponde en sus dimensiones, propiedades y características a la pirámide ilustrada por el Símbolo Perfecto.
Al comparar las dimensiones calculadas para el plano de la pirámide modelo, con las medidas tomadas en la Gran Pirámide, podemos constatar que son exactamente iguales. ¿No es asombroso que la estructura de la Gran Pirámide refleje las mismas medidas, características y propiedades que nos ilustra el Símbolo Perfecto? La única posibilidad que existe es que los egipcios usaron el diseño del Símbolo Perfecto para crear la estructura de la Gran Pirámide. ¿Quién podría imaginarse que con un sólo número puedan definirse todas las dimensiones de la Gran Pirámide?
Según explicado ya, pero para darle énfasis a la presentación: entre un infinito de números, solamente existe uno que satisface el radio del círculo, o altura de la Gran Pirámide, para que se puedan generar correctamente las medidas de la Gran Pirámide. Curiosamente este número se genera como el producto de 153 y expresado en pies. Si no se usa ese número, las medidas de la pirámide no serán iguales. Cuando se varíe el valor del radio, cambiarán las dimensiones de la “pirámide modelo” y de la Gran Pirámide. Por tanto, hay un solo valor exacto para el radio, que satisface la creación de todas las dimensiones correctas de la Gran Pirámide.
Al comparar todas las secciones del plano de la “pirámide modelo” sección a sección, a las dimensiones medidas en la Gran Pirámide, veremos que son exactamente iguales. ¿Ya pronto veremos lo interesante que resulta la razón, del por qué los factores tienen que ser exactamente 153 pies y el valor de Pi? ¿Además, por qué utilizar unidades de pies, si los egipcios usaban codos egipcios como medida?
En mi estudio yo no tuve el problema de calcular el ángulo de las caras, el “Símbolo Perfecto” esta ya definido, y el ángulo corresponde a 51° 49’ 38.25”. Usando este ángulo y la medida considerada correcta de los lados según Petrie, la altura de la Gran Pirámide es igual a 480.6637 pies, exactamente el numero usado para mi diseño de la Gran Pirámide.
Al utilizar un radio equivalente a 480.6637 pies, el plano nos indica las siguientes dimensiones básicas para la “pirámide modelo” y que representará el plano oficial de la Gran Pirámide.
La altura de la pirámide = 480.3667 pies
Los lados de la base de la pirámide = 755.7488 pies
La medida inclinada del tope de la pirámide al centro de su base = 611.41 pies
El ángulo de las caras de la pirámide = 51.82729319° = 51° 49’ 38.25”
Por otro lado, los resultados obtenidos de las mensuras directas realizadas en la estructura de la Gran Pirámide por diferentes agrimensores son:
La altura de la pirámide = 480.75 pies
Los lados de la base de la pirámide = 755.75 pies
La medida inclinada del tope de la pirámide al centro de su base (la apotema) = 611.41 pies
Nota: Un dato curioso que encontré en mi visita al Vaticano, en Roma, Italia, y el cual vale señalar, es que se colocó una placa de información en la Nave Central de la Basílica que indica que la longitud de la nave principal era de (186.36 metros) = 611.41 pies, curiosamente esa es la medida de la apotema de la Gran Pirámide. Se comenta que ninguna otra Basílica en el mundo puede ser mayor que ésta.
El poder diseñar y establecer el diseño del plano completo de la Gran Pirámide, sin siquiera tomar en consideración las dimensiones, características o propiedades de la estructura de la Gran Pirámide, representa una seria, e inequívoca realidad, de que el plano geométrico sugerido por el Símbolo Perfecto es el origen de la Gran Pirámide y que realmente constituye su plano de construcción.
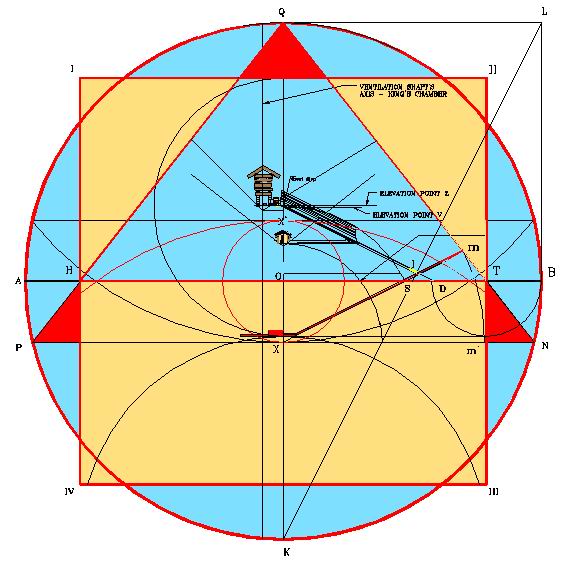
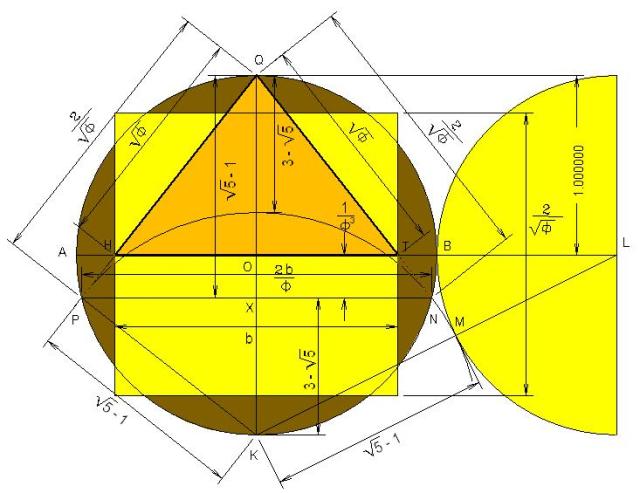
UTILIZANDO UN RADIO DE 480.6637 PIES SE CREAN TODAS LAS DIMENSIONES DE LA GRAN PIRAMIDE
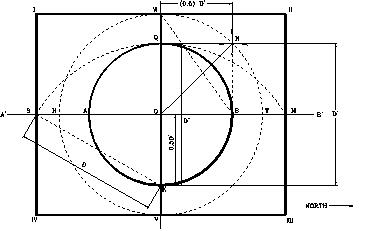
Además, podemos señalar que este nuevo plano de la Gran Pirámide diseñado por Samuel Laboy independientemente de sus dimensiones, es mucho más preciso y confiable que el plano arbitrario construido con las medidas obtenidas en el Monumento, por agrimensores, e investigadores de las pirámides. La pasada figura representa el diseño del plano de la Gran Pirámide diseñado por Laboy utilizando únicamente el Símbolo Perfecto, mediante el radio igual a (153 El plano, resuelve, además, muchas de las incógnitas sobre el diseño de la Gran Pirámide. Por ejemplo, el diseño de la subestructura de cámaras y pasillos debajo de la pirámide, cosa que nadie ha diseñado. El punto señalado como X, representa, si dividimos el diámetro vertical en dos partes, el que crea la proporción de f = 1.6180339. En la figura humana representa la base de los genitales (que representa satisfacción, eternidad, placer, poder, reproducción), creando el sitio perfecto para construir la Cámara Mortuoria oficial del Faraón. En este sitio, debajo de la cámara subterránea, en el centro del eje de la pirámide (no de los pasillos) sería el sitio apropiado para el Faraón construir su Cámara Mortuoria y guardar sus tesoros.
EVIDENCIA ADICIONAL DE QUE EL SÍMBOLO PERFECTO ES EL ORIGEN Y A LA VEZ, EL MARCO DE LA ESTRUCTURA DE LA GRAN PIRÁMIDE
FINALMENTE, EL SIMBOLO PERFECTO FUE EL CREADOR DE TODAS LAS PIRAMIDES DE EGIPTO
FORMULAS PARA DETERMINAR LAS DISTANCIAS EN EL SIMBOLO PERFECTO
Multiplique el valor que usted desee para el radio del círculo, en las unidades de medidas preferidas, por la formula entre los puntos requeridos y obtendrá el resultado en las unidades de medida del radio.
Basta calcular las dimensiones que se generan con el ya determinado radio para el plano sin dimensiones para compararlas con las dimensiones existentes en la estructura. En esta ocasión, a través de fórmulas matemáticas que desarrollé mediante el Símbolo Perfecto, podemos calcular las distancias existentes entre los puntos correspondientes en el símbolo, y que corresponden a las que existen entre las partes correspondientes en Pirámide. Para ello, utilizaremos las formulas en unidades de, y segúnilustradas en la figura siguiente.
FORMULAS PARA DEFINIR DISTANCIAS ENTRE DOS PUNTOS DEL SIMBOLO PERFECTO Y ENTRE LOS CORRESPODIENTES A LA ESTRUCTURA DE LA GRAN PIRAMIDE DE EGIPTO
Formulas desarrolladas por el Ing. Samuel Laboy a base de la función de Phi == 1.6180339…
Nota: Un gran beneficio de las fórmulas desarrolladas por Samuel Laboy es que muchos de los resultados de esas medidas sólo pueden obtenerse mediante sus fórmulas. Significa que no hay modo en que físicamente puedan ser medidas en el interior de la estructura.
Para calcular la distancia entre dos puntos de la pirámide, multiplique el valor de la fórmula por la unidad de medida que usted interese usar como radio del círculo y que será equivalente a la altura de la Gran Pirámide. Por ejemplo: A continuación se muestran los resultados de las formulas, para las diferentes secciones señaladas en el dibujo para un radio (R), equivalente a 480.6637 pies.
- La apotema de la pirámide. Se define como la distancia inclinada desde el ápice, o tope al centro de la base en el pavimento. Ilustrada desde el punto Q al punto H, o desde el punto Q al punto T. Formula = (√f) (R) = (√f) (480.6637) = 611.41 pies
- Distancia inclinada desde el punto K al punto P, o desde el punto K, al punto N. Formula = (√5 -1) (R) = (√5 -1) (480.6637)= 594.1330 pies
- Distancia horizontal del punto P, al punto N. Formula = (4 R / √f3) = (4) (480.6637) / (√f3) = 934.1569 pies
- Distancia vertical del punto Q al punto X. Formula = D / f = (2) (480.6637) / f = 594.1330 pies
- Distancia vertical del punto Q al punto X’. Formula = D / f2 = (2) (480.6637)/ f2 = 367.1944 pies
- Distancia vertical del punto X’ al punto X. Formula = D / f3 = (2) (480.6637)/ f3 = 226.9386 pies
- Distancia vertical del punto O, al punto X: Formula = R / f3 = 480.6637 / f3 = 113.4693 pies
- Distancia inclinada del punto Q al punto P, o del punto Q, al punto N. Formula = D / √f = (2) (480.6637)/ 1.27201965 = 755.7488 pies
- Distancia vertical del punto X al punto K. Formula = (3 – √5) (R) = (3 – √5) (2) (480.6637) = 367.1944 pies
Las dimensiones calculadas muestran las distancias correctas entre los dos puntos determinados en la estructura virtual del símbolo y que proporcionalmente corresponden a los puntos iguales en la estructura de la Gran Pirámide.
En mis dos libros, “A Civil Engineer looks at the Great Pyramid” y en el “Suplemento” podrá ver una comparación detallada sobre estas dimensiones que demuestran que son iguales. No obstante, sabemos que las medidas tomadas de las construcciones terminadas difieren ligeramente en algunas ocasiones de las medidas originales estipuladas en los planos. Esto es debido a las dificultades y problemas que se crean durante la construcción de las obras. Por eso, son identificadas como “las medidas originales del plano”, y las “medidas tomadas de la construcción”.
Esta presentación, definitivamente, prueba de forma final, que con un radio de 480.6637 pies en el “Símbolo Perfecto, se origina el plano de la estructura de la Gran Pirámide, y que el símbolo representa el patrón geométrico que enmarca su diseño.
Los datos y detalles geométricos sobre los diseños de la entrada original a la pirámide, de la Cámara del Rey y sus cinco techos, de la Cámara de la Reina, de la Antecámara, de la Gran Galería, y de los llamados canales de ventilación, son presentados con detalles en mis dos libros sobre la Gran Pirámide, el Original y su Suplemento. Es importante mencionar que lo dicho aquí no es una teoría o ideas, esto es algo real que puede ser comprobado fácilmente por los interesados.
En el video “Modern Evaluation of the Great Pyramid”, Parte I, mostrado en “YouTube”, se demuestra que el diseño creado con el Símbolo Perfecto corresponde exactamente al plano de construcción de la Gran Pirámide. La parte II del video muestra la comparación entre las medidas de los dos diseños envueltos, y la parte III, muestra el gran conocimiento de los egipcios en geometría, y donde hacen galas de la solución de problemas matemáticos complejos utilizando la geometría.
Creo ser una persona afortunada al ser la única que ha diseñado completamente la Antecámara con el Símbolo Perfecto, que es realmente la “llave” para diseñar toda la Gran Pirámide. Lo usé para diseñar la entrada original a la Gran Pirámide, la Cámara del Rey y sus cinco techos, la Cámara de la Reina, la Gran Galería, y los ángulos y longitudes, de los llamados canales de ventilación. Por consiguiente, también podemos establecer que el plano geométrico sin dimensiones es prueba irrefutable de que es el origen de la estructura de la Gran Pirámide y que el mismo representa su plano geométrico de construcción. De mi parte, creo firmemente en los conocimientos y aplicación del Símbolo Perfecto por los diseñadores egipcios, pues mediante su uso, también pude exponer el diseño geométrico de las pirámides de Chephren, Micerino, la Pirámide Roja y la Pirámide Romboidal, entre otras.
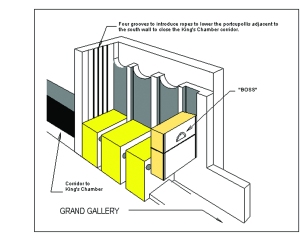
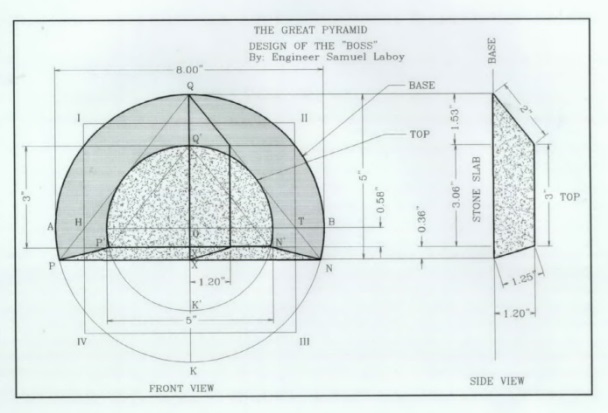
Algo que considero muy importante en las construcciones con bloques de piedra, y que no han sido estudiados científicamente, son los llamados sobresalientes, o tallados realizados sobre los lados de los bloques de piedra. Algunos eruditos los llaman en inglés (construction bosses) los cuales son construidos de varias pulgadas de alto y de espesor, los cuales, se dice, tenían el propósito de facilitar la transportación y manipulación de los bloques de piedra, mediante el amarre de sogas o cuerdas, a esos puntos. De mi parte, difiero de esos señalamientos y no veo el por qué en el Documental no dicen nada al respecto pues éstos son muchos y son claramente ilustrados en el Documental. Por lo menos, deberían presentarse algunos argumentos válidos para explicar su construcción. Son tan intrigantes como las uniones entre los bloques.
En referencia a estos sobresalientes, uno de ellos que se la ha dado mucha relevancia por un lado, y poco interés en investigar por el otro, es el tallado sobre la cara de la losa superior de granito, de dos colocadas una sobre la otra, a la entrada de la Antecámara en la Gran Pirámide. Este sobresaliente siempre ha sido descrito por egiptólogos y eruditos como sin valor y sin interés alguno. En cambio. Para mí, como ingeniero, tiene otra perspectiva. Frecuentemente los ingenieros identifican sus diseños y obras mediante placas de identificación. Estoy seguro que los diseñadores y constructores de una obra de la calidad y grandeza como la Gran Pirámide, pensarían como los de ahora, dejando un mensaje al futuro, sobre su excelsa creación.
Este sobresaliente, mide una pulgada de espesor y es parecido a la forma y tamaño de una herradura de caballos en su forma semicircular, tiene un radio de aproximadamente 4 pulgadas, y ángulos laterales con inclinación hacia el centro. Fue trabajado recortándole 1 pulgada a toda la cara del bloque de piedra, para dejar expuesta una superficie liza dejando una pulgada de roca para tallar el objeto. Sabemos que no hay forma en que se pueda amarrar una cuerda a este objeto con el propósito de arrastrar, o sostener el bloque de piedra. Es el único sobresaliente construido de esta forma, entre los cientos o miles, que se han construido sobre bloques de piedras.
Para mí la aparición de este objeto ha sido una bendición. Al diseñar la Antecámara utilizando el Símbolo Perfecto, las dimensiones del salón resultaron ser iguales a las usadas en su construcción. Al diseñar la entrada de la Antecámara, mi diseño mostró como debían colocarse las dos piedras de granito y la posición y forma de posicionar un mensaje sobre el bloque de piedra que identificara la terminación de la pirámide y su construcción basada en el Símbolo Perfecto.
La forma, dimensiones y construcción de la entrada a la Antecámara, fue realizada por los egipcios exactamente según mi diseño. El objeto tallado era igual al trazado y estaba localizado en el sitio prescrito. La forma del objeto era exactamente la del Símbolo Perfecto, pero ilustrando únicamente la parte del diseño geométrico de la Gran Pirámide. Eso no podía ser casualidad. Llevé mi descubrimiento a varios egiptólogos para su interpretación y evaluación. Entiendo que por motivos de desconocimientos matemáticos, de diseño, y de geometría, se negaron a estudiar y evaluar la presentación de este, el único mensaje intencional dejado escrito en piedra por nuestros antecesores, sobre la construcción de la Gran Pirámide.
DESIGN OF THE ANTECHAMBER’S ROOM
La situación encontrada respecto al sobresaliente en la Antecámara, fue tan impresionante para mí, que le envié copia de mi diseño y un modelo en madera del sobresaliente que construí del objeto que fue tallado, como evidencia, al Dr. Zahi Hawass en Egipto, quien era el Director del programa sobre las pirámides. Mi intención era que se salvara y protegiera dicho objeto, por su gran valor histórico. Nunca recibí contestación alguna de Egipto.
De mi parte creo que es muy posible que otros sobresalientes que se tallaron sobre los bloques de piedra en Egipto, Perú, y en otros lugares, tengan o indiquen algún tipo de mensaje que no sabemos interpretar.
En mi libro “Suplemento” presento todo el diseño, paso a paso de toda la Antecámara. Increíblemente, todo cae según especificado. En mi visita a las pirámides en Egipto en 1983, mi atractivo principal fue el visitar la Antecámara y observar y analizar personalmente este valioso objeto.
LA FUNCION DE PI = π
π La constante generalmente identificada con la letra griega p, representa la relación numérica entre la circunferencia de un círculo y su diámetro. El valor de p es equivalente a 3.14159… Su decimal ha sido calculado a billones de sitios decimales sin que se le haya encontrado el fin. Generalmente su valor se abrevia como 3.1416. Se dice que la función de π y la de f, fueron creada y usada por Nuestro Creador como parámetros para proporcional los objetos en el firmamento. La función de π es equivalente a 3.14159… donde sus números decimales no tienen fin. Generalmente y por conveniencia, el número es reducido a 3.1416. Esta función es usada en matemáticas, geometría, y en construcciones. La circunferencia de los círculos, es igual al producto entre π y el diámetro del círculo, en formula, C = D π.
LA FUNCION DE PHI = f
f De otra parte, la llamada Proporción de Oro, La Divina Proporción, el Número de Oro, la función de Fi y otros nombres, es corrientemente identificada en Matemáticas y en geometría con la letra Griega f, y es equivalente a 1.6180339… Al igual que la función de π, sus números decimales nunca terminan. La función de f es parte fundamental del Símbolo Perfecto y es la que le da belleza y simetría a los diseños. Si los egipcios conocían la función de f y sus propiedades, y quisieran integrarla en su sistema, todo lo que tenían que hacer era establecer la proporción entre el valor del codo y la función de f. El famoso egiptólogo Jean Leclant, indica en sus conferencias que cree que los egipcios usaron a f, pero lo mantuvieron en secreto.
EL NÚMERO 153 – EN LA GRAN PIRAMIDE
153 Mi interés y estudio sobre las pirámides de Egipto surgió como resultado de la constante manifestación, en mis actividades diarias y por muchos años consecutivos, del número 153. Este número surgía con demasiada frecuencia en mis cómputos matemáticos en mis trabajos de ingeniería. Se reflejaba insistentemente ante mi vista en rótulos, en licencias de autos, en artículos en revistas, en todo lo que representaba números. Aún en mis viajes a diferentes países podía percibir este raro fenómeno. No es que estuviera pendiente del número, o lo estuviera buscando. Era algo irregular, fuera de las estadísticas esperadas.
Al número 153 se le atribuyen determinadas características curiosas. Por ejemplo, en la Sagrada Biblia, en el Libro de San Juan 21:1, se menciona que la tercera vez que Jesús se presentó a sus discípulos después de su resurrección, fue junto al mar de Tiberías, luego de una noche en la que los discípulos no pescaron nada. Cuando ya iba amaneciendo, Jesús se les presentó y los orientó a echar la red a la derecha de la barca para hallar los peces. Luego de los discípulos hacerlo, casi no podían sacar la red del mar por la gran cantidad de peces que contenía. Simón Pedro sacó la red a tierra ante la presencia de Jesús, estaba llena de grandes peces, 153, y aun siendo tantos, la red no se rompió.
Recuerdo un determinado día, hace más de 40 años, en el cual me interesé en leer mi primer libro sobre la Gran Pirámide de Egipto. Ese día, el número 153 se me había manifestado en varias ocasiones. En la lectura del libro me llamó la atención el dato de que la Gran Galería tenía una longitud de 153 pies. ¡Ahí estaba el número otra vez! Aunque eso no era cosa de preocupar a nadie, para mí la repetición del número en ese momento llenó la copa. Tenía que hacer algo para determinar la razón de la coincidencia, casualidad, o lo que fuera, para encontrar la razón de mi constante relación con ese número. Se me ocurrió encontrar la contestación en las lecturas sobre la Gran Pirámide, por lo que decidí continuarlas. Seguí adquiriendo libros sobre la Gran Pirámide y continué mis lecturas. Por pura intuición se me ocurrió pensar que la altura de la pirámide era representada por el producto del número 153, y el símbolo que representa el círculo, es decir Pi (= π = 3.141592654…). El producto era igual a 480.6637 pies. Desconocía por completo la altura de la Gran Pirámide. Encontré que la altura provista por la referencias era variable, dependiendo del libro que usara. De todas formas, la medida era muy aproximada a los 480 pies y podía considerar el resultado como correcto. Interpreté que la intuición era un mensaje para que estudiara y determinara la geometría verdadera de la pirámide. ¿Cuál sería el siguiente paso a dar? Se me ocurrió que para crear el diseño de la pirámide debía utilizar el patrón geométrico arquitectónico usado por los egipcios para el diseño de la Pirámide. Me di a su búsqueda por varios años, sin resultados positivos. Finalmente conseguí diseñar mediante el uso de un compás y un tiralíneas, sin utilizar números, o cómputos, el patrón arquitectónico y geométrico que buscaba. Utilizando el patrón geométrico, que llamé el Símbolo Perfecto, por sus grandes propiedades para diseñar obras, logré diseñar el plano de una pirámide modelo de la Gran Pirámide, sin utilizar dimensiones. No obstante, tendría que determinar, entre una infinidad de números y unidades de medida, el número que correspondiera a generar todas las dimensiones del plano que había diseñado sin números. Recordé mi previo encuentro con el 153 (π) = 480.6637 pies y lo use para la altura de la pirámide. Al calcular todas las secciones de la pirámide modelo y compararlas con las medidas que se han tomado de la estructura de la Gran Pirámide, me di cuenta que era exactamente igual a las dimensiones, características y propiedades que tenía la Gran Pirámide. En otras palabras, tenía en mis manos el plano original de la Gran Pirámide de Egipto.
Aunque sé que la distancia entre dos puntos es igual, aunque se midan usando diferentes unidades de medidas, tenía que definir la razón por la cual los codos egipcios fueron presentados usando unidades de pies.
Se conoce que las unidades de medida de los egipcios eran los codos y que su medida menor era un (1) codo. Digamos que los egipcios conocían las virtudes de la función de f y sus variaciones. Para relacionar los dos sistemas, hacen una proporción directa donde la nueva unidad es: 1 codo / f = 0.6180339 codo, pero como necesitan una regla de 12 codos, la longitud sería igual a 1 codos / f =1 codo. O sea, deberían construir una regla de 12 codos:
12 codos / f = (12 / f) = 7.416407865 (codos)
Pero, de acuerdo a las unidades de codos egipcios, dos científicos famosos, Isaac Newton y Sir W. Petrie, calcularon y concluyeron que el valor del codo egipcio era igual a 20.63 pulgadas.
Por lo tanto, 7.416407865 (codos) = 7.416407865 (20.63) = 153.000 pulgadas.
Como consecuencia, la regla de madera tenía 153 pulgadas pero representaban 7.416407865 codos. Significa que al medir usando el largo de la regla en codos = 7.416407865 (codos), estaban midiendo 153 pulgadas, en base al sistema inglés.
Como (12 / fcodos), es equivalente a 153 pulgadas, si lo egipcios interesan una regla mayor de medir, por ejemplo exactamente de 12 codos, la regla mediría 153 (f) =12 codos =247.5592 pulgadas.
En otra manera más sencilla, como 7.416407865 (f) = 12 codos egipcios, 153pulgadas multiplicado por (f), equivale a 12 codos egipcios.
Como 153 pulgadas es igual a (12 / f) codos, una regla de 12 codos sería igual a 153 (f) = 247.5592 pulgadas, o sea, los agrimensores egipcios tendrían disponibles una regla de 12 codos.
Por ejemplo si ellos usaron la regla de 7.416407865 codos (= 153 pulgadas para medir la longitud del techo de la Gran Galería, la cual mide 153 pies, hubiesen tenido que medir 12 veces el largo de la regla, es decir, 12 x 153 = 1,836 pulgadas = 153 pies. Como sabemos, la longitud del techo de la Gran Galería es de 153 pies, número que confirma el largo de 12 reglas de 153 pulgadas.
Las medidas tomadas por Mr. Petrie en la Gran Pirámide podrían ser otra evidencia sobre lo dicho sobre los codos egipcios. Petrie señala que la distancia vertical desde el pavimento al techo de la antecámara mide 153 pies. Lo cual podemos pensar que esta distancia vertical representa 12 unidades exactas de medidas de 153 pulgadas, o de 7.416407865 codos. Petrie también indica que la medida de la altura de la Antecámara desde el piso a al techo es de 153 pulgadas. En estos dos casos, pero en muchos más en la pirámide, pueden observarse la distancia de 153 pulgadas y la de 153 pies, utilizadas como unidad de medida. Toda esta relación matemática, es producida por la función de f, la que considero fue integrada en el sistema de codos egipcios y se refleja en el sistema inglés por la equivalencia señalada.
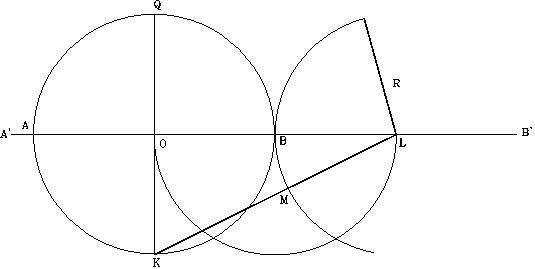
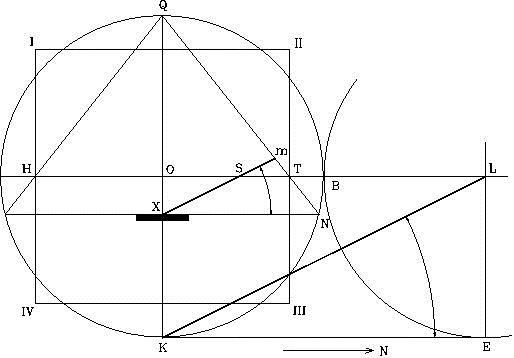
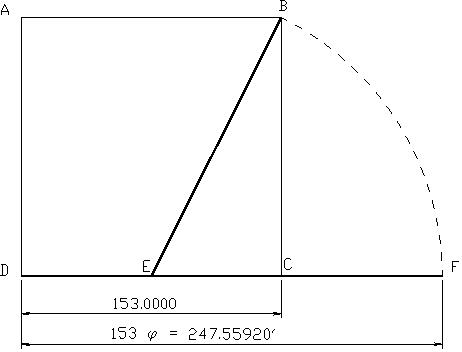
Mediante la siguiente formula geométrica los egipcios podían construir sus reglas de 12 codos, con la función de f ya integrada,
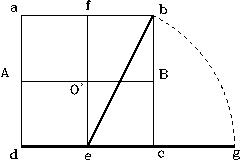
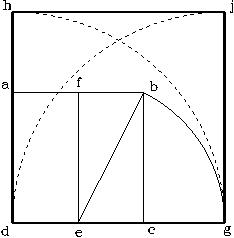
Proceda de la siguiente forma:
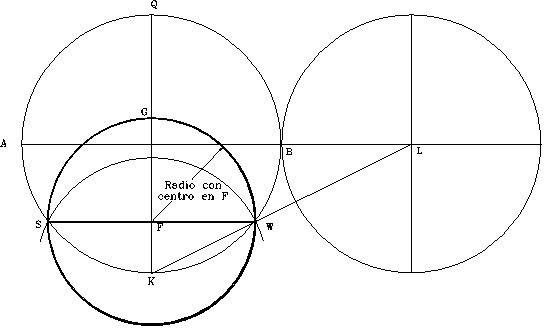
La figura nos muestra un cuadrado (ABCD) con lados de 153 pulgadas (= 7.416407865 codos). Con un compás colocado en el punto E en el medio de la línea DC, y radio EB, trace un arco hasta interceptar la extensión de la línea DC en el punto F. La longitud de la línea DF será igual a 153 multiplicado por f = 247.5592 pulgadas. También (7.416407865) f =12 codos.
Note that the length of the circumference of a circle having the length of the ceiling of the Grand Gallery, represents the height of the Great Pyramid (153) (3.14159) = 480.6637 ft.
153 (π) ft.= 480.6637 ft. – Great Pyramid’s height
153 inches = (12) (1 / f) cu = (12) (0.6180339 cubits) = 7.416407865 cubits
1 cu = 153 (f) / 12 = 20.63 inches
1 cu = (7.416407865) (f) / 12
12 cu = [(12) (7.416407865) (f)] / 12
153 ft. = 153 (12) in = 1,836 in
1,836 in / 20.63 = 88.996 cu
C = 88.996 (π) = 279.59 cu
1 cu = 1.719161113 ft.
These numeric equivalencies represent great findings, especially for the Egyptologists, if they desire to explain the manifestation of the number 153 in the Egyptian units of measurements and in the Great Pyramid.
For example, to use Egyptian cubits: R = 153 (π) = 480.6637 ft.
The radius (R) in ft. and changed to cubits: (480.6637 ft.) (12 in) = 5,767.9641 inches,
From the other part (5,767.9641 inches / 20.63) = 279.5911 Egyptian cubits.
To solve the formulas and obtain the results in Egyptian cubits, use R = 279.5911 cu. and calculate the entire dimensionless plan, or use Laboy’s formulas.
GEOMETRIA DEL AREA RECTANGULAR PARA CONSTRUIR LAS TRES PIRAMIDES DE GIZA
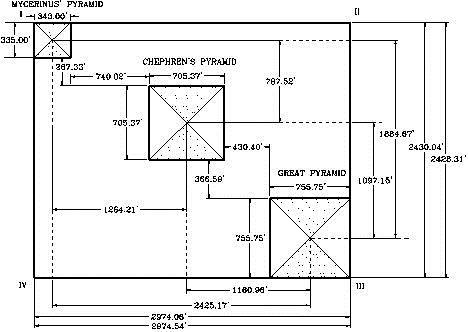
El área rectangular utilizada para construir las tres grandes pirámides de Giza, conocidas como la Gran Pirámide, construida por el Faraón Cheops, la segunda, construida por el faraón Chephren, y la tercera por Micerino, tiene su origen en un diseño geométrico sencillo y fácil de trazar. No voy a entrar en el proceso de construcción de esas tres pirámides, solamente hacer los tres diseños geométricos, independientemente, pero usando el mismo sistema. En mi libro podrá ver los detalles completos de los diseños.
FÓRMULA PARA DEFINIR EL ÁREA UTILIZADA EN GIZA PARA LA CONSTRUCCIÓN DE LAS TRES GRANDES PIRÁMIDES
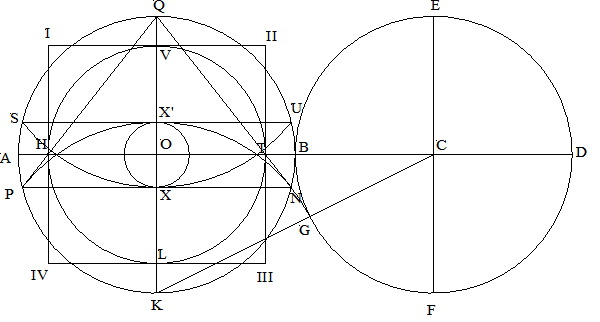
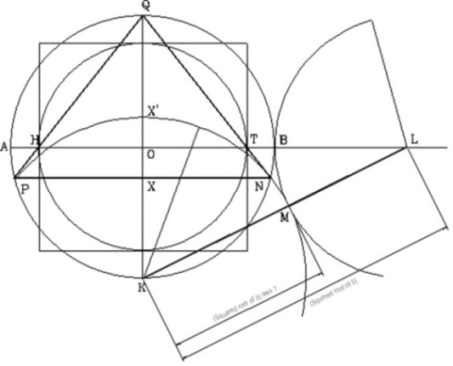
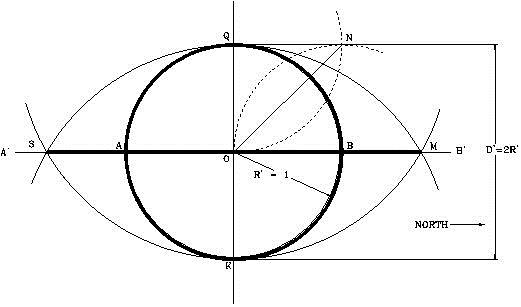
Trace un círculo con sus diámetros horizontal y vertical. Localizando un compás en Q y con radio QK, trace un semicírculo. Localice el compás en K y con radio KQ trace otro semicírculo. Marque los puntos S y M en la línea horizontal A’B’.
Coloque el compás en el punto Q y con radio QO trace un arco que intercepte otro arco igual desde el punto B, en el punto N.
Coloque el compás en el punto O y con radio ON trace un circulo. Trace un rectángulo utilizando la distancia SM de longitud y la altura igual a KV.
El diámetro de circulo = D = dos veces la altura de la pirámide + la medida de sus lados
La longitud del rectángulo (I, II, III, IV) = D ( )
El ancho del rectángulo = D ( )
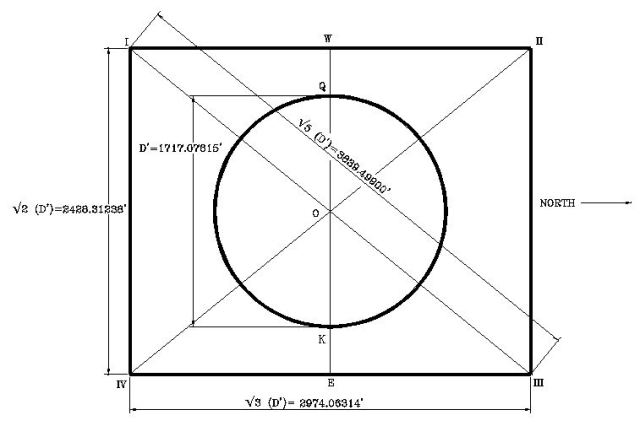
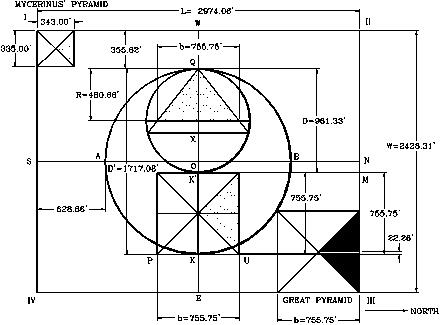
La longitud del rectángulo de terreno para localizar las tres grandes pirámides de Giza será igual a la raíz cuadrada de 3 multiplicado por el diámetro del círculo interior = (D) = 2,974.063 pies
Mientras que el ancho será igual a la raíz cuadrada de 2 multiplicado por = (D) = 2,428.312 pies.
El diámetro (D) del circulo interior será igual a la suma del diámetro del Circulo para diseñar la Gran Pirámide, más la medida de los lado de la base cuadrada de la pirámide, = (480.6637) (2) + 755.7488 = 1717.0762 pies.
En resumen:
L = 2,974.063 pies
W = 2,428.312 pies
La distancia diagonal del rectángulo = (D) = 3,839.4989 pies
Las medidas de este rectángulo son iguales a las medidas tomadas por Sir W. M. Petrie para el rectángulo, según posteriormente ajustadas por un error en las medidas de la base de la Pirámide de Micerino.
MEDIDAS ENTRE LOS CENTROS DE LA CONSTRUCCION DE LAS TRES PIRAMIDES
Según medidas por Sir W. M. Petrie
Las medidas concuerdan exactamente con mi diseño.
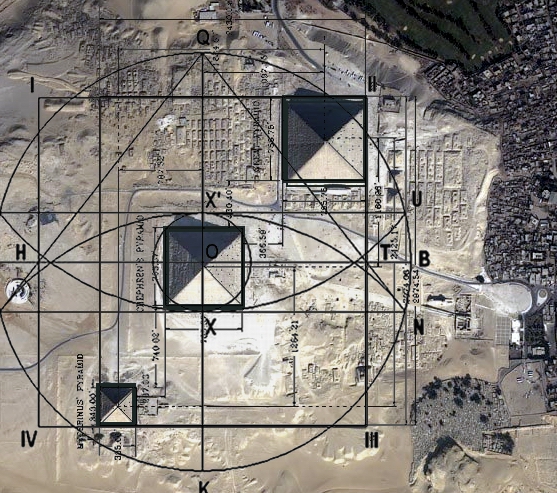
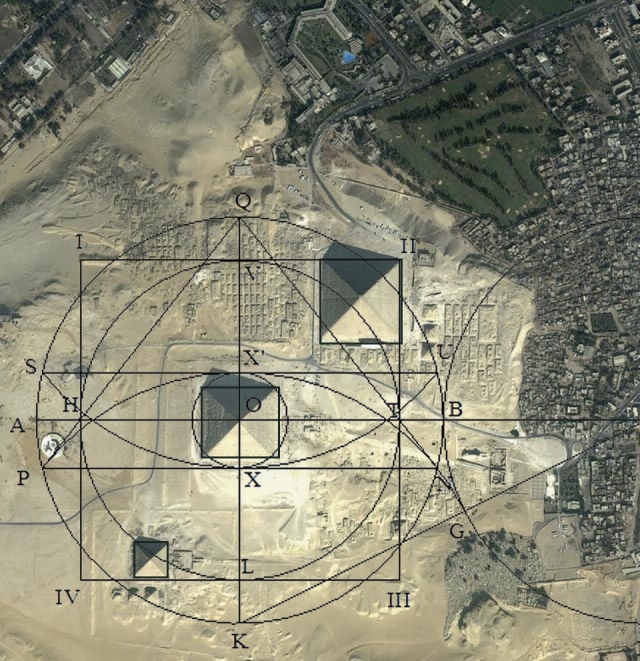
Observe como el área del rectángulo diseñado anteriormente, enmarca perfectamente las tres grandes pirámides de Giza, donde la esquina superior derecha queda definida por la Gran Pirámide, y la inferior izquierda por la pirámide de Micerino. Tanto mi diseño del área rectangular para construir las tres pirámides, como el Símbolo Perfecto que también fue superpuesto, enmarcan perfectamente el área en que fueron construidas las tres Pirámides.
Podrá notarse que el centro de la pirámide de Chephren es el centro del Círculo.
Observe que el Símbolo Perfecto enmarca perfectamente las tres grandes pirámides de Giza, donde el centro del círculo queda localizado en centro de la pirámide de Chephren. La esquina superior del cuadrado del símbolo enmarca la Gran Pirámide, mientras que la Pirámide de Micerino está localizada en el lado de abajo del cuadrado. Observe en la esquina superior izquierda, un tipo de construcción larga, que aparentemente marca la esquina izquierda superior del cuadrado. El lado horizontal de la pirámide de Micerino y el lado derecho de la Gran Pirámide, establecen la otra esquina del cuadrado.
En este caso, el centro de trabajo de las pirámides en Giza, queda localizado en el centro de la segunda pirámide, es decir, la de Chephren. Tomando ese punto en especial, las tres pirámides pueden ser ubicadas y construidas usando el Símbolo Perfecto.
AREA RECTANGULAR PARA LA CONSTRUCION DE LAS PIRAMIDES DE GIZA
Medidas calculadas por Samuel Laboy Dimensiones medidas por Petrie
L = 2,974.063 pies L = 2,974.063 pies
W = 2,428.312 pies W = 2,428.312 pies
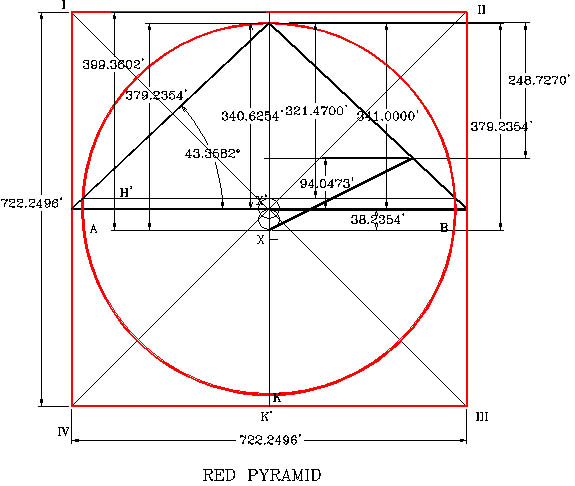
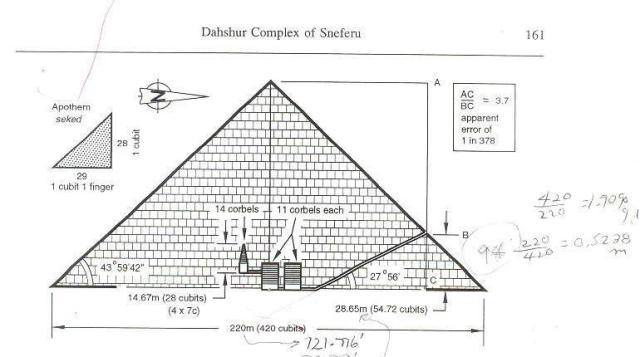
LA PIRÁMIDE ROJA
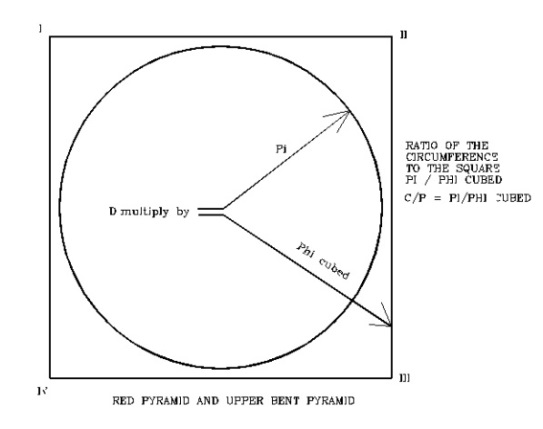
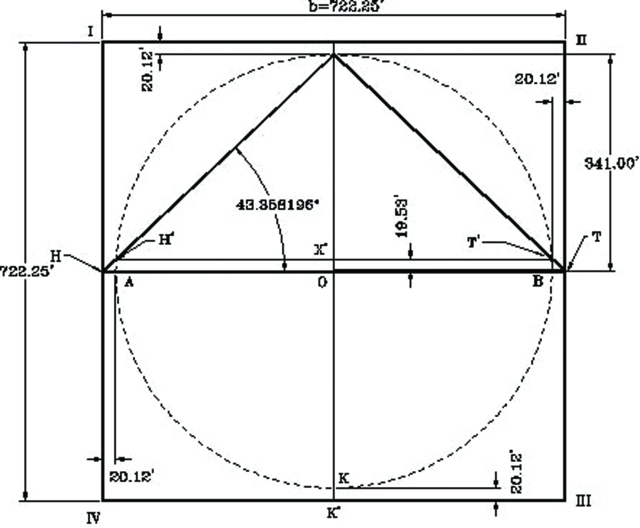
El diseño de la Pirámide Roja, tiene unas propiedades únicas y nunca mencionadas por los investigadores. Estas se muestran en el dibujo ilustrativo y son las siguientes: Su base queda localizada fuera de los límites del círculo que la genera, y otra es una propiedad muy especial. El producto del diámetro del círculo y el valor de π, resulta, como es conocido, en el valor de la circunferencia del círculo, es decir, C = D π, pero aquí podemos observar un dato propio de una persona que conoce mucho los procesos geométricos. Cuando se multiplica el mismo valor del diámetro por el valor de f3 al cubo, (= D f3), el resultado nos da el valor del perímetro (P) del cuadrado de la base (P = 4 (b). Este concepto es único y fue usado por el visier-ingeniero de Sneferu, llamado Inhotep, en el diseño de esta pirámide y en la pirámide modelo que forma la sección superior del diseño de la Pirámide Romboidal.
C = D π D f3 = P = 4b
La proporción entre la circunferencia y el perímetro de las pirámide es igual a: C / P = π / f3,
C / P = D π / P = D π / D f3 =π / f3
C / P = π / f3, P = C (f3) / π, P =D (f3) π / π = D (f3)
C / (b) π = (4 / f3) = D π / (b) π = D / b,
Como R= 341.00 pies, D = 2 (341.00) = 682.00, b = 722.25 pies
(D / b) = 0.94427137, pendiente del ángulo de la pirámide
El ángulo de la pirámide = 43.35818132 = 43 21’ 30”
Aunque el ángulo de esta Pirámide se informa igual a 43° 36′ 11″, es más probable que el original fuera 43° 21′ 30″, el cual es igual al de la sección superior de la Pirámide Romboidal, que como veremos, su diseño consiste de la superposición de los diseños de dos pirámides. Es importante señalar que el ángulo de 43° 21′ 30″ representa, el ángulo establecido por el diseño. Este ángulo podría variar ligeramente respecto al ángulo que se obtendrá al medirlo en la obra. Sabemos que es extremadamente difícil mantener exacto el ángulo de un diseño durante la etapa de construcción de estas obras grandes como las pirámides, especialmente con la limitación en instrumentación para mensuras durante esa época.
No hay duda que tenemos que aceptar ciertas tolerancias, aunque pequeñas en sus dimensiones de ángulos y medidas. En mi opinión, es más importante el determinar que ángulo se pretendía establecer en la obra, que obtener la medida actual, de una estructura deteriorada, construida hace cinco siglos.
EL IMPORTANTE VALOR DE LA FUNCION DE f³
Por otro lado, es tanta la referencia al valor de (f³) en la Pirámide Roja y en la configuración geométrica de la sección superior de la Pirámide Romboidal, que merece una explicación más detallada de mi parte. El valor de (f³) está presente en la fórmula (D / b) = (4 / f³) que aplica a la configuración de estas dos pirámides en particular, y que representa la inclinación de las caras de la pirámide.
Podemos interpretar de las fórmulas que la pendiente del ángulo de las caras es (D / b) = (4 / f³) = 0.94427191, el cual corresponde a la función de la tangente del ángulo 43.35819755 o sea, 43 21’ 30”.
De acuerdo con las referencias, los lados de la Pirámide Roja tienen una longitud de 722.25 pies. Por lo tanto, su altura, de acuerdo a mi fórmula sería igual a h = R = (2 b / f3) = (2) (722.25) / (f3) = 341 pies. La altura de esta pirámide se informa en algunas referencias como 343 pies [Ref. #13, Edwards, I. E. S., Pág. 90], y como 4,111 pulgadas = 342.58 pies por Piazzi Smyth. No obstante, debido a la pobre exactitud en su construcción y el deterioro sufrido a través de los años, considero que mi cálculo para la altura es el correcto.
LEONARDO DA VINCI Y LAS PIRAMIDES OCULTAS
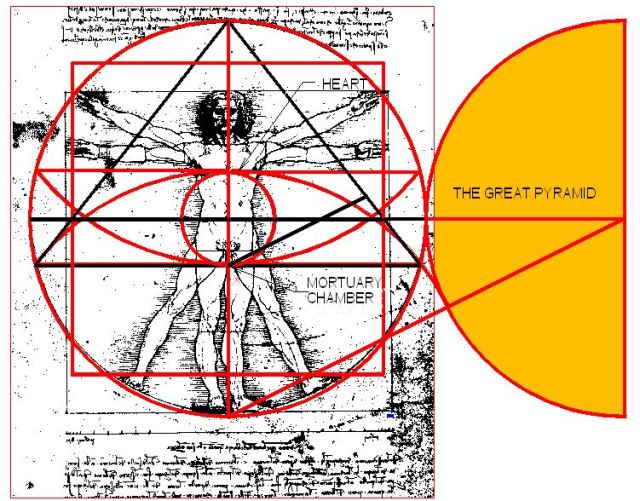
El Símbolo Perfecto trazado por el ing. Samuel Laboy nos muestra
los diseños de la Gran Pirámide y la de Micerino
Ocultas en el dibujo de Leonardo.

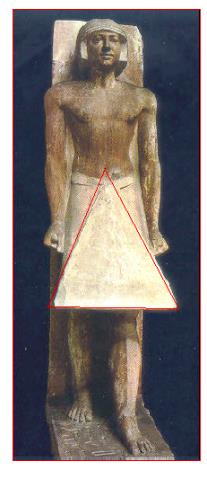
La pirámide de Micerino, además la figura representa el diseño de la falda utilizada por los hombres egipcios.
Las estatuas representan la costumbre de los hombres de usar faldas triangulares
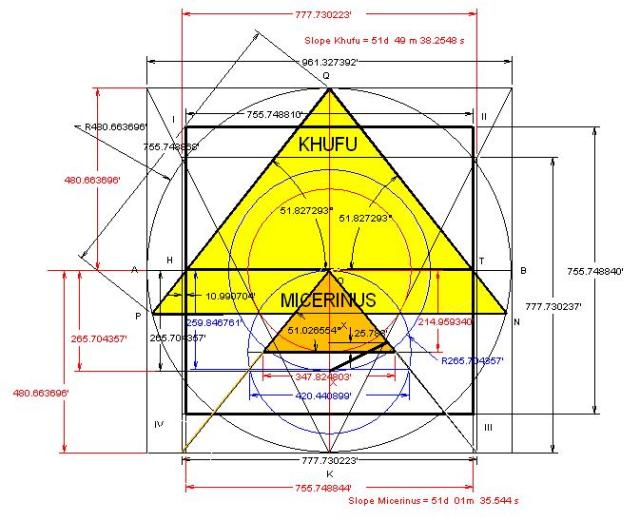
La figura representa un análisis que define las dimensiones y proporciones del Símbolo Perfecto en relación al dibujo de Leonardo, la Gran Pirámide y la de Micerino.
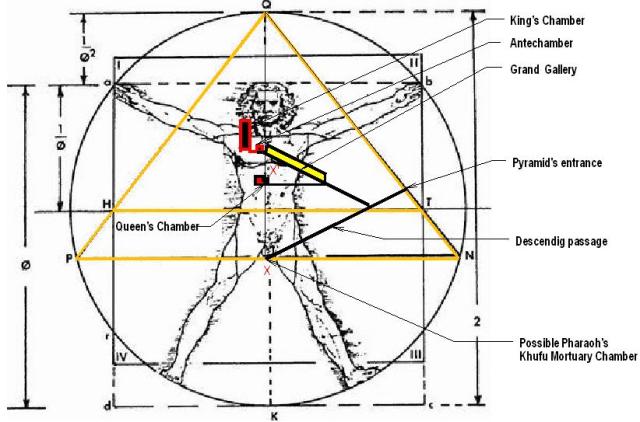
LA CONFIGURACION DE LA PIRAMIDE
EN EL DIBUJO DE LEONARDO DEFINE LA LOCALIZACION DE:
LA CAMARA DEL REY
DE LA CAMARA DE LA REINA
LA CAMARA SUBTERRANEA
Y PROBABLEMENTE EN LOCALIZACION DESCONOCIDA
LA CAMARA MORTUORIA DEL FARAON CHEOPS
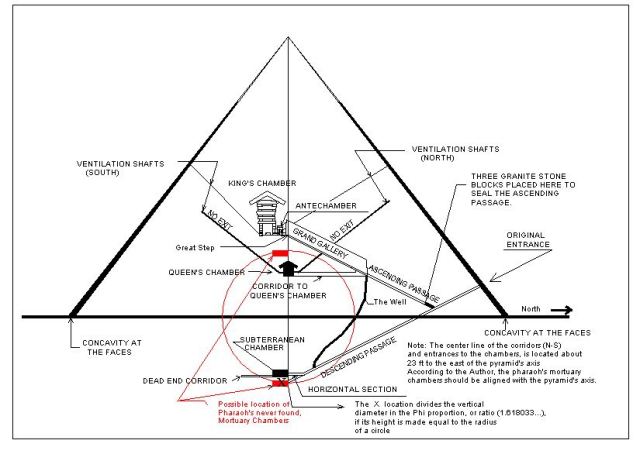
Las dos posibilidades de localizar la camara Mortuoria del Fraraon Cheops
Los dos puntos Phi del Símbolo Perfecto
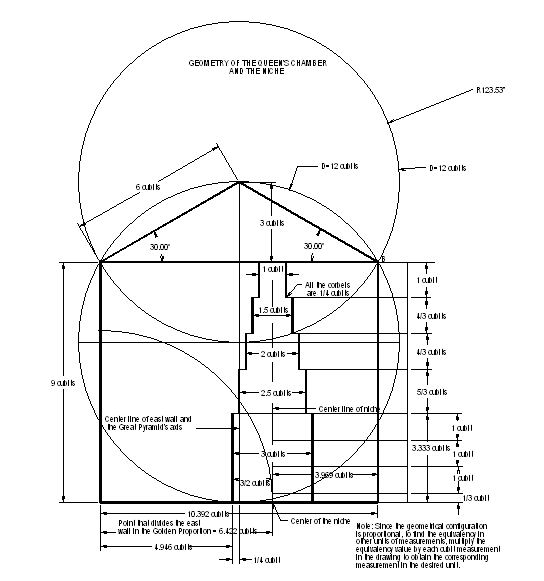
DISENO DE LA CAMARA DE LA REINA EN LA GRAN PIRAMIDE
Digno de verse y de evaluar su contenido. (Vease el libro)
DISEÑO GEOMETRICO DE LA PIRAMIDE DE CHEPHREN
Dibuje dos círculos tangentes en B, y trace línea KL. Marque el punto W. Coloque el compás en K y con radio KW trace un arco hasta interceptar la circunferencia en S.
Trace un circulo con FS y marque el punto G en su intersección con el diámetro vertical.
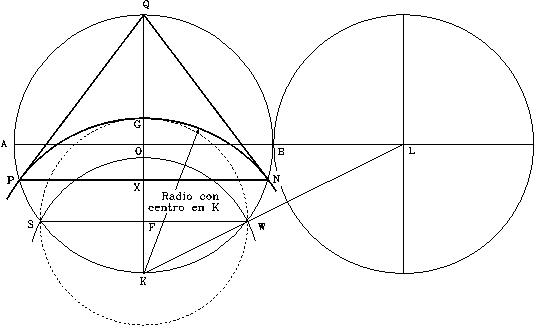
Coloque el compás en el punto K, y con radio KG trace otro arco que corte la circunferencia del circulo en P y N. Trace las líneas inclinadas QP y QN. Trace la línea horizontal PN y marque el punto X.
Con un radio = 150 () = 471.24 pies, calcule las dimensiones de la figura y obtendrá las dimensiones y el ángulo correspondiente a la pirámide de Chephren.
DISENO GEOMETRICO DE LA PIRAMIDE DE CHEPHREN
Sus dimensiones son iguales a las de la pirámide de Chephren en Giza.
DISENO GEOMETRICO DE LA PIRAMIDE DE MICERINO
PIRAMIDE DE MICERINO
Dimensiones calculadas para la Pirámide de Micerino:
Altura de la Pirámide = R = h = 213.92 pies
Longitud de los lados = b = f (R) = 346.13 pies
Circunferencia = C = p D =(p / f) (2) (b) =
= (p) (2) (213.92) = 1,344.10 pies
Perímetro de la base = D (2 f) = 4 (b) = 4 (346.13) = 1,384.52 pies
Tangente del ángulo q = tan q = (D / b)= (213.92) (2) / 346.13 = = 1.23608 = (Ö5 – 1)
Angulo de las caras = q = 51.02655° = 51° 01′ 36″
Distancia vertical = OX = 44.47 pies
[Ref. #43]: Estudio de Sir W. M. Petrie (1881-82) sobre la pirámide de Micerino
Altura de la Pirámide = h = Varía entre 212.42 a 214.92 pies
Longitud de los lados = b = 4,153.6 pulgadas = 346.13 pies
Inclinación de las caras = q = 51° 00′ (más o menos 10′)
El ángulo de inclinación = q = Correcto entre 50 ° 50′, y 51° 10′
Formulas desarrolladas por el ingeniero Samuel Laboy para las pirámides más importantes de Egipto (basadas en la función f)
R= radius D = diameter C= circumference f = 1.6180339…
Face slope = (D / b) Face angle = Tan inv. (D / b)
PYRAMID SLOPE SIDE LENGTH HEIGHT ANGLE
D / b (b) (R) ° /’ /»
——————————————————————————————————
Khufu Öf (D / Öf) = 2R / Öf (b Öf) / 2 51.82729337°
51° 49′ 38.3″
Chephren (4Ö2) / f³ (f³ R Ö2)/ 4 2Ö2 b / (f³) 53.17273225°
53° 10′ 21.8″
Mycerinus 2 / f (R) (f) (b) / f 51.02655266°
51° 01′ 35.5″
Red Pyramid 4 / f³ (R) f³ / 2 (2 b) / f³ 43.35819755°
43° 21′ 29.51″
BENT PYRAMID
PYRAMID SLOPE SIDE LENGTH HEIGHT ANGLE
Lower angle = Ö2 = (R) Ö2 = (b) / Ö2 54.73561032°
54° 44′ 8.2″
Upper angle = 4 / f³ = (R) f³ / 2 = (2 b) / f³ 43.35819755°
43°21′ 29.51″
—————————————————————————————————————
Known b = 620.00 ft.
Lower Angle – Extended – height (b) / Ö2 = 620.00 (Ö2) = 876.8124 ft.
Known b = 722.25 ft.
Upper Angle Extended – Height 2 (b) / f³ = 2 (722.25) / f³ = 341.00 ft.
————————————————————————————————————-
Examples: Calculations of the pyramid’s heights:
Height
PYRAMID OF KHUFU = (b Öf) / 2 = (755.7488) (1.27201965) / 2 = 480.66366 ft.
Known b = 755.7488 ft
PYRAMID OF CHEPHREN= 2 Ö2 b / (f³) = 2 Ö2 (705.76) / f³ = 471.24 ft.
Known b = 705.76 ft
PYRAMID OF MYCERINUS = (b) / f = 335 / f = 207.04 ft., (345) / f = 213.22 ft.
Known b = 335.00 ft.
Known b = 345.00 ft.
RED PYRAMID = (2 b) / f³ = (2) (722.25) / f³ = 341.00 ft.
Known b = 722.25 ft.
Bent Pyramid: Lower Face Ratio = Ö2 = 1.414213562
Bent Pyramid: Lower Face Angle = 54.73561032° = 54° 44’ 8.197”
Bent Pyramid: Upper Face Ratio = 4 / f³ = 0.94427191
Bent Pyramid: Upper Face Angle = 43.35819755° = 43° 21’ 29.51”
Note: The pyramid of Chephren’s angle corresponds to the product of the two superimposed, upper and lower pyramid models, which composed the Bent pyramid’s design.
Bent Pyramid’s upper section ratio = (4 / f³)
Bent Pyramid’s lower section ratio = Ö2
Chephren’s Pyramid: Face Ratio = (Ö2)(4 / f³) = 1.335402142
Chephren’s Pyramid: Face Angle = 53° 10′ 21.8«
Red Pyramid: Face ratio = 4 / f³ = 0.94427191
Red Pyramid: Face Angle = 43° 21’ 29.51”
Links:
Website: http://www.samuellaboy.com/
YouTube Channel: https://www.youtube.com/channel/UCcvHnif3DSx-qeEq__-6kUA


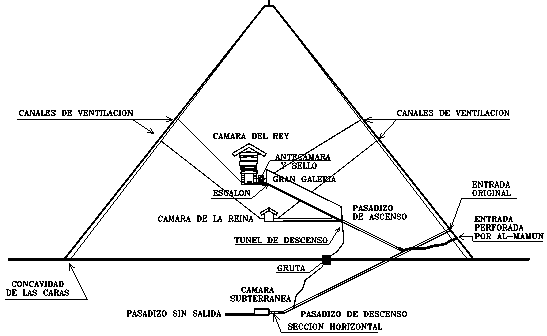




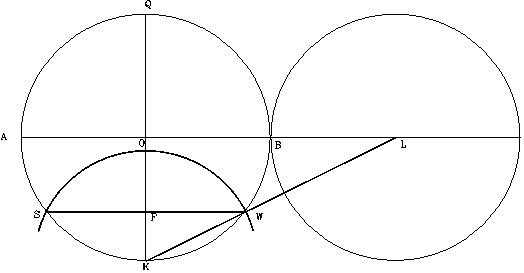



Los antiguos egipcios no tenian ese conocimiento , no conocian esa geometria tan compleja, todos esos numeros, no sabian nada de eso, los antiguos egipcios no conocian la geometria, la geometria como ciencia, la geometria abstracta, la inventaron-descubrieron los griegos muchos siglos despues. Pero a la vez es irrefutable que las construyeron siguiendo estos modelos matematicos, esta contradiccion a mi entender representa el mayor misterio, sin resolver aun, de las piramides de Giza
Los Egipcios solo restauraron las piramides. Lo que nos cuentan en los libros es un cuento chino, la verdad es otra y seria muy dificil cambiar la historia de mas de 2000 años.
Tambien es otro cuento chino la forma de construccion que nos describen los libros, teniendo algo de sentido comun simplemente te das cuenta de la mentira.
La verdad pudo haber estado escrito en aquellas antiguas bibliotecas que ya fueron destruidas para continuar con el misterio.
Si, pienso lo mismo. Por eso el articulo presente, que geometricamente el Sr. Laboy ha descubierto su patron matematico de construccion.
Si, solo las restauraron, esto esta claro, muy claro.
Pingback: ¿Por qué llamamos al 2016 el AÑO GRANDE a nivel CABALÍSTICO? / Sábado 31 de Octubre-Halloween y Domingo 1 de Noviembre-Día de Todos los Santos, nuevas fechas OCA a OCA o con numerosas CONEXIONES CABALÍSTICAS!! / España cada vez más cerca del mism
Pingback: ¿Por qué llamamos al 2016 el AÑO GRANDE a nivel CABALÍSTICO? / Sábado 31 de Octubre-Halloween y Domingo 1 de Noviembre-Día de Todos los Santos, nuevas fechas OCA a OCA o con numerosas CONEXIONES CABALÍSTICAS!! / España cada vez más cerca del mism